Volume of Pyramids and Cones

Introduction

The volume of a pyramid or cone is equal to 1/3 the area of its base times its height. If a pyramid and cone have the same height and their bases have the same area, then their volumes will be the same.

In these pages you will learn why this formula works (in particular, why we must multiply by 1/3).

You will see that a triangular pyramid is 1/3 of a triangular prism. That is, a triangular prism can be split into three triangular pyramids with the same volume, so each pyramid has 1/3 the volume of its shared prism.

Then you will see that any pyramid can be split into triangular pyramids, so again the volume is 1/3 the area of its base times its height.

Finally, a cone must also have the same volume formula, because it could be made from slices of a pyramid of the same height and same cross-sectional areas. This idea is known as Cavalieri's Principle.

Cavalieri's Principle

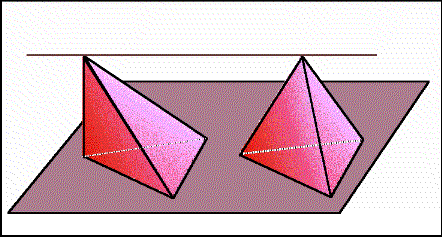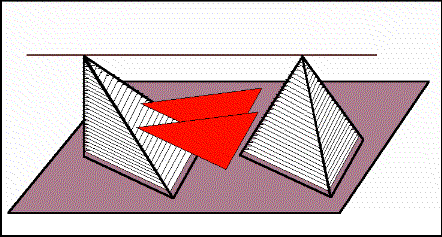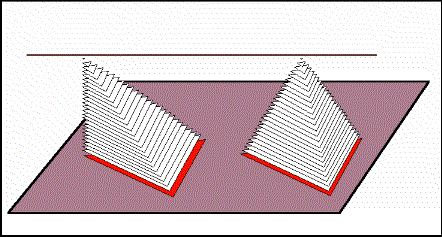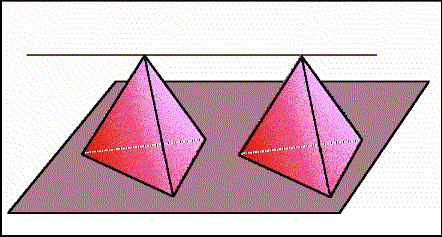
These two pyramids have the same height and congruent bases.

If we imagine them constructed of stacks of paper triangles, we can reconfigure the triangles of the pyramid on the left so it becomes the same as the pyramid on the right. This idea is based on Cavalieri's Principle: Two objects with the same heigth and the same cross-sectional areas have the same volume.

Volume of a Triangular Pyramid (Tetrahedron)

The illustration here shows how a triangular prism (tetrahedron) can be cut into three triangular pyramids, each having the same volume. The drawing is based on Euclid's Proposition 7 from Book XII. It follows that the volume of one such pyramid is 1/3 of the volume of the prism with a base and altitude in common with the pyramid.

You can view Euclid's proof online: Book XII Proposition 7

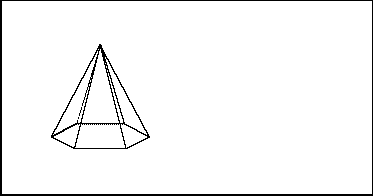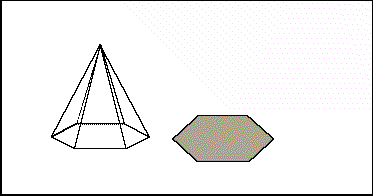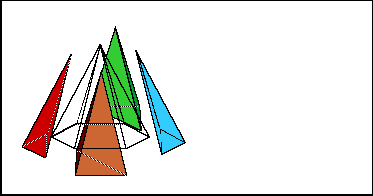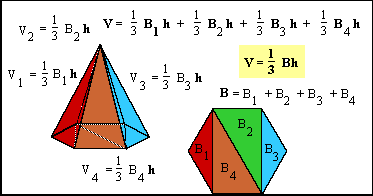
Volume of Any Pyramid

The illustration here shows that any pyramid can be split into triangular pyramids. Since the volume of a triangular pyramid is 1/3 its base area times its height, it follows that the volume of all of them is 1/3 the area of the original pyramid's base times its height.

You can view Euclid's proof online: Book XII Proposition 6

Volume of a Cone

The illustration here demonstrates that the volume of a cone with the same base-area and same height as a pyramid is the same as the volume of the pyramid. This must be true by Cavalieri's Principle (two objects with the same cross-sectional areas and height must have the same volume).

You can view Euclid's proof online: Book XII Proposition 10

Return to Lesson 13