Perpendicular and Parallel Constructions

Perpendicular to a Line at an External Point

Given a line and a point not on that line, we will construct a perpendicular line through the given point.

Recall that points on the perpendicular bisector of a segment are equidistant from the endpoints of the segment.  So we will mark off a segment whose endpoints are equidistant from the given point by drawing part of a circle centered at the given point.

Set the compass at any convenient length more than the distance from the point to the line, place the tip on the point and cut the line with part of the circle to mark the endpoints of segment AB:

Then construct the perpendicular bisector of segment AB: 

Here is an animation of this construction.

Perpendicular to a Line at a Point on the Line 

When the given point is on the given line, you need only mark off a segment that contains the point as its midpoint and then construct the perpendicular bisector of that segment:

Set the compass at any convenient length and mark arcs of the circle with the given point as its center and intersecting the line at points A and B: 

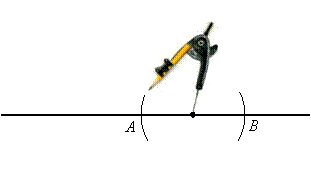
Then open the compass a little more and construct the perpendicular bisector of segment AB:

Here is an animation of this construction.

Perpendicular at the Vertex of a Ray

If the point where you want to construct a perpendicular is the vertex of a ray or endpoint of a segment, then you simply use the straight-edge to extend the ray or segment so the point is no longer the endpoint and do as before: make the point the midpoint of some segment and construct the perpendicular bisector of that segment.

Given:  Segment AB

Construct a line perpendicular to AB through point A.

Solution:

Place the straight-edge along AB (points A and B determine only one line) and extend the segment to any convenient length to point C so that A is between C and B: 

Then place the point of the compass at A and pencil at C to measure the distance AC, and mark off point D between A and B using an arc of this radius:

Finally, construct the perpendicular bisector of CD:

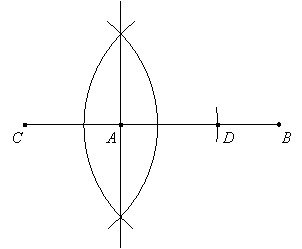
Another method is to make use of the fact that an angle inscribed in a semicircle is a right angle:

Here is an animation of that method.

A Parallel to a Line through a Point

Given a line and a point P not on that line, you can construct a parallel through P by making congruent corresponding angles for a transversal through that point.  First you make the transversal (any line through P that cuts the given line):

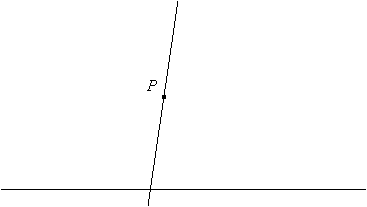
 Then you copy the angle at the line to an angle with vertex at P:

Here is an animation of this construction.

Another way to Construct a Parallel

The following method is somewhat easier if you wish to construct an accurate parallel to a line through a given point not on the line.  The idea is to make the opposite side of a rectangle with the given line on one side.

First construct a line perpendicular through the given point:

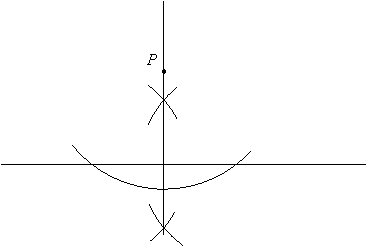
Then construct another perpendicular a convenient distance from this perpendicular:

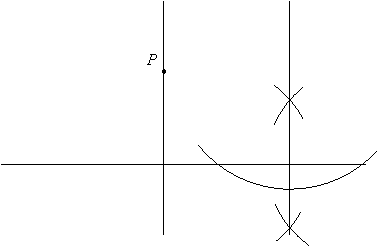
Then set the compass to the distance from the line to P and mark off that distance on the newly constructed perpendicular:

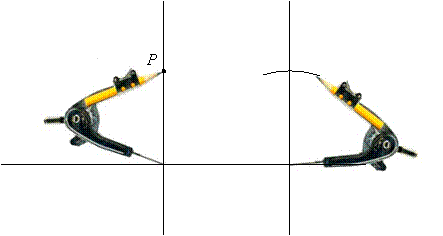Finally draw the parallel through P and the new point: 

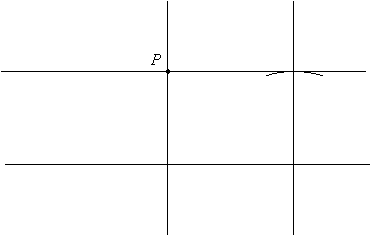Divide a Segment into n Equal Parts 

Parallel lines can be used to divide a segment into equal parts as the following example illustrates.

Given:  Segment AB, locate points P, Q, R, and S so AP = PQ = QR = RS = SB.

Solution:  Draw any angle less than 45^o with vertex A and copy that angle in the reverse direction at vertex B:

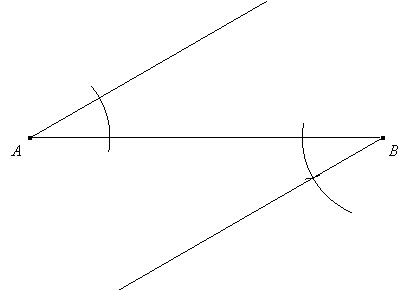
Then set the compass at any convenient length and mark off 4 equally-spaced points on the new sides of each angle, starting at each vertex. 

Finally, connect those points in order with lines that intersect AB at points P, Q, R, and S:

Here is an animation of this construction done slightly differently.

Return to Lesson 9