Scaling

Suppose a rectangle measures 2 inches by 3 inches and a similar rectangle is twice as long.  Then that other rectangle measures 4 inches by 6 inches.  The perimeter of the second rectangle is twice the perimeter of the first rectangle because 4+6+4+6=2 times (2+3+2+3), but the area is 4 times as great.  When we construct a similar figure by a scaling factor of s, all linear measures of the scaled figure will be s times as great as the original figure, but the area will be s² times as great.  This applies to three-dimensional figures as well as two-dimensional figures.

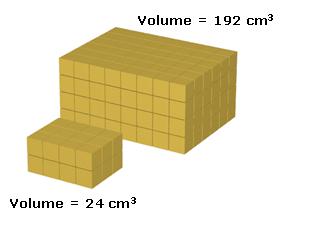
Now suppose we have two boxes.  The first is 4 cm long, 3 cm wide, and 2 cm high as in our previous example, and the second is a scaled version with a scaling factor of 2.  Then all linear measures of the scaled box will be twice as long as the corresponding measures of the original, all area measures will be 4 times as great, and the volume will be 8 times as great:

In 1638 Galileo wrote his final book, The Discourses and Mathematical Demonstrations Relating to Two New Sciences, a scientific testament covering much of his work in physics over the preceding thirty years.  Galileo proposed a new science, the study of the strength of materials, that considered how the size and shape of structural members affects their ability to carry and transmit loads. He discovered that as the length of a beam increases, its strength decreases, unless you increase the thickness and breadth at an even greater rate. You cannot, therefore, simply double or triple the dimensions of a beam, and expect it to carry double or triple the load. This led Galileo to recognize what we now call the scaling problem:  There are limits to how big nature can make a tree, or an animal, for beyond a certain limit, the branches of the tree or the limbs of the animal, will break under their own weight. 

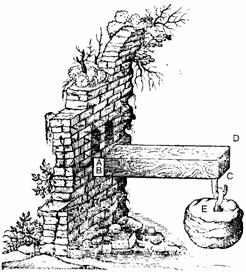The main point was that the strength of a beam or other elongated object, such as an arm or the limb of a tree, is proportional to the area of a cross-section, whereas its weight is proportional to its volume.  Galileo argued if a rock almost but not quite heavy enough to break a beam of a certain thickness is hung from a beam and then another rock of twice that size is hung from another beam twice as long and thick, the second rock will break the second beam because its weight has increased by a factor of 8, whereas a cross-section of the beam has only increased by a factor of 4.  In other words, a large structure proportional in exactly the same way as a smaller one must necessarily be weaker.  The illustration on the right is from Galileo's last book.

As a consequence, movie characters like King Kong couldn't exist because they would collapse under their own weight.

 

toc | return to top | previous page | next page