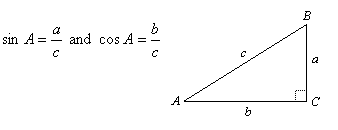
The Law of Cosines
A Pythagorean Relation between Sine and Cosine
If ABC is a right triangle with right angle C, then
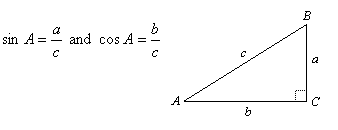 |
If we add the squares of sin A and cos A, we have:
![]()
But a2 + b2 = c2 by the Pythagorean Theorem. Therefore (sin A)2 + (cos A)2 = 1. In other words, the sum of the squares of the sine and cosine of the same angle will equal 1. This is true for any angles (not just acute angles).
A Generalization of the Pythagorean Theorem
In triangle ABC, if C is a right angle, then the Pythagorean Theorem tells us c2 = a2 + b2:

But what if C is not a right angle?
First suppose C is less than 90o. Draw an altitude from B to AC:

By the Pythagorean Theorem, c2 = x2 + h2, and h2 = a2 – y2, so c2 = x2 + a2 – y2. But x + y = b, so x = b – y, and therefore c2 = (b – y)2 + a2 – y2 = a2 + b2 – 2by. Now
![]()
So finally:
![]()
Now suppose C is greater than 90o. By similar reasoning, we again find that
![]()

This makes use of the fact that cos(180o – θ) = –cos θ as can be seen when θ is in standard position:

The following examples show how the Law of Cosines can be used to find missing parts of triangles.
Example 1:
Find the length of the side marked x:

Solution:
Since x is opposite the given angle, the Law of Cosines gives us:

Example 2:
Find the length of the side marked x:

Solution:
This is an SSA case, so there might be more than one answer and we will have to be careful. Since 9 is opposite the given angle, the Law of Cosines gives us:
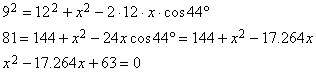
Now we use the quadratic formula to find x:
![]()
So there are indeed two possible values of x:

Example 3:
Find the value of θ:

Solution:
Since θ is opposite the side of length 22, the Law of Cosines tells us:

Another Area Formula
A remarkable formula discovered by the ancient Greeks tells us how to find the area of any triangle when only the side lengths are known. It is known as Heron's Formula, and involves the semi-perimeter, s. It can be proved using methods similar to the derivation of the Law of Cosines, but involves a lot of algebraic simplifications. A more interesting proof is given in the next activity.

Example 4:
Find the area of the triangle with side lengths 8, 9, 11

Solution:
First we find the semi-perimeter:
![]()
Then:

Example 5:
Check Heron's formula for a right triangle whose sides measure 3, 4, 5.
Solution:
