Inverse Trig Functions

The Inverse Functions

From the general definitions, a trig function of any two angles that are coterminal will have the same values.  In addition, since the absolute value of a trig function of an angle is equal to the trig function of its reference angle, there would be an infinite number of angles for which a certain trig function has a specified value.  For this reason, the inverses of the trig functions are defined with restricted ranges:

Example 1:

Solution:

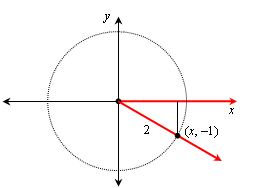
The triangle formed by the perpendicular from the point on the terminal side to the x-axis has hypotenuse 2 and leg 1, so it is a 30-60-90 triangle, and the other leg has length the square root of 3.  The 30^o angle is the reference angle, so θ = –30^o:

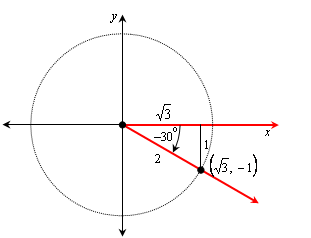
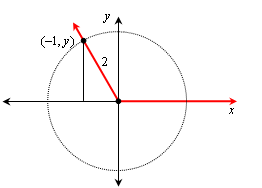
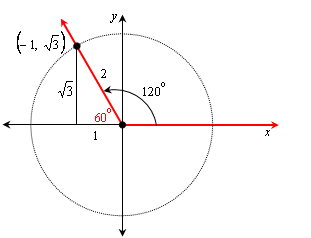
The triangle formed by the perpendicular from the point on the terminal side to the x-axis has hypotenuse 2 and leg 1, so it too a 30-60-90 triangle, and the other leg has length the square root of 3.  The 60^o angle is the reference angle, so θ = 120^o:

Example 2:

Solution:

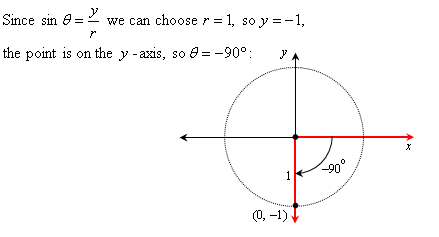
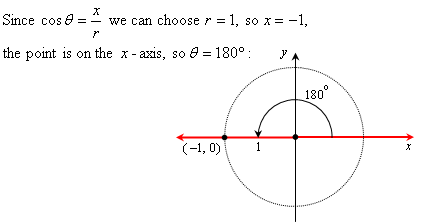
Example 3:

 Find θ to the nearest degree if 180^o < θ < 270^o and sin θ = –0.96126.

Solution:

 If α is the reference angle, then sin α = 0.96126.  Using a calculator, we find: 

α = sin^–1 0.96126 = 74^o to the nearest degree, so θ = 180^o + 74^o = 254^o:

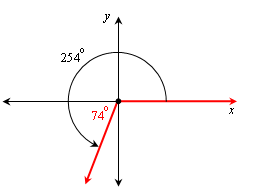
Example 4:

Solution:

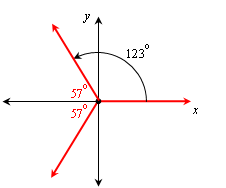
Since cos^–1x must be between 0^o and 180^o, we our answer will be an angle in quadrant 2 with the same reference angle as 237^o, so we draw pictures to find the answer:

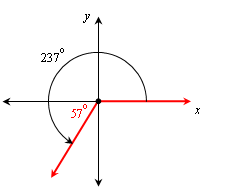
The reference angle is 237o – 180o = 57o, so we draw an angle in the second quadrant with that reference angle, and then find that θ = cos^–1(cos 237^o) = 180^o – 57^o = 123^o: