Heron's Formula

The Formula

Heron's formula is one of the most remarkable results discovered by the ancient Greeks.  It tells you how to find the area of any triangle given only the measures of the sides.  What you do is find half the perimeter, called s (for "semi-perimeter"), subtract the length of each side from that, multiply s by those three quantities, and take the square root:

Example:

This formula can be derived by splitting the triangle into six triangles with vertices at the center of its inscribed circle and making use of an interesting formula involving tangents of angle that add to 90^o.

Done this way, there are two steps, which will be explained in detail.

Tangent Formula

Our first formula can be understood from the following diagram: 

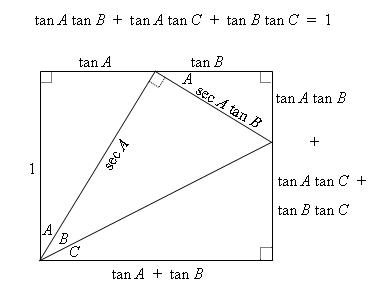
Derivation of Tangent Formula

Then we can use this formula to arrive at Heron's formula by applying it to the angles labeled with the Greek letters α, β and γ as follows:

Derivation of Heron's Formula

Return to Lesson 15