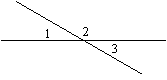
Finding Angles
Intersecting Lines

1. Consecutive angles are supplementary: Angles 1 and 2 add to 180o.
2. Vertical angles are congruent: Angles 1 and 3 are congruent.
EXAMPLE 1: If angle BPC is four times as large as angle CPD, then what is the measure of angle APB?
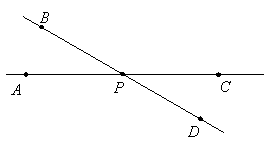 |
SOLUTION: If x is the measure of angle CPD, then 4x is the measure of angle BPC:
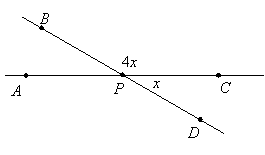
Angles BPC and CPD are supplementary, so 4x + x = 180. Therefore 5x = 180, so x = 36. That is, angle CPD measures 36o. Angles APB and CPD are vertical angles and therefore congruent. So angle APB measures 36o.
EXAMPLE 2: Find the values of x and y:
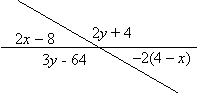 |
SOLUTION:
Using vertical angles, we know that 2x – 8 = –2(4 – x)
The right side simplifies to –8 + 2x or 2x – 8 so this equation is an identity:
2x – 8 = 2x – 8
Any number makes this true, so we cannot find x directly.
Again by vertical angles, 2y + 4 = 3y – 64. This equation is not an identity and we can solve for y:
4 = y – 64
68 = y
So we know y = 68, and therefore the two angles containing ymeasure 2(68) + 4 = 140o.
Since the angle marked 2x – 8 is supplementary to this angle, we now know
2x – 8 = 140, so 2x = 148, and therefore x = 74.
Parallel Lines
When two parallel lines are cut by a transversal, there are 8 pairs of congruent angles and 8 pairs of supplementary angles. This can be understood by identifying a pair of corresponding angles, and using vertical angles and linear pairs. Corresponding angles can be thought of as angles that match when a picture of one angle at the intersection of one of the parallel lines with the transversal is moved to the other parallel line:
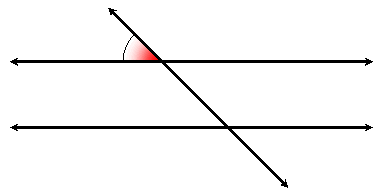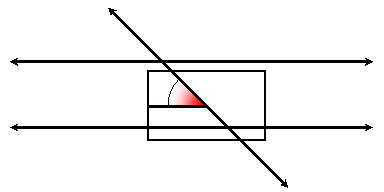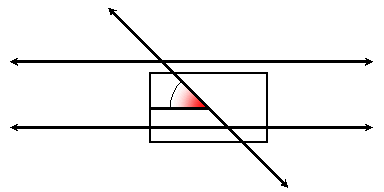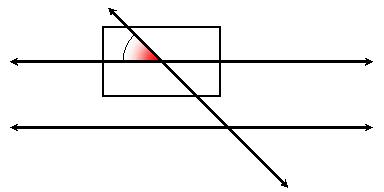
The following summarizes angle congruences for two parallel lines cut by a transversal:
 |
All other pairs of angles (that is, pairs marked with an even and an odd number) are supplementary.
EXAMPLE 3: Find x and y if lines a and b are parallel, and determine if lines c and d are parallel.
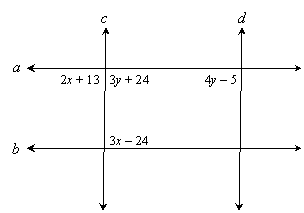 |
SOLUTION: Since a and b are parallel, 2x + 13 = 3x – 24 (they are alternate interior angles). Solving gives x = 37.
These angles measure 2 . 37 + 13 = 87 degrees, and the angle marked 3y + 24 is supplementary to this, so 3y + 24 = 93.
Solving this equation gives y = 23.
Then 4y – 5 = 92 – 5 = 87, which again is supplementary to 3y + 24.
Since these are same-side interior angles for lines c and d cut by transversal a, lines c and d are parallel.
Parallelograms
A parallelogram is a quadrilateral in which opposite sides are parallel. Pairs of interior angles are either congruent or supplementary:
 |
Opposite angles are congruent (angles 1 and 3, and angles 2 and 4).
Consecutive angles are supplementary (angles 1 and 2, angles 2 and 3, angles 3 and 4, and angles 1 and 4).
EXAMPLE 4: Could the following figure be a parallelogram?
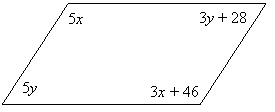 |
SOLUTION: If it is a parallelogram, then 5x = 3x + 46 since opposite angles are congruent.
Solving gives x = 24, so 5x = 120.
If it is a parallelogram, then 5y = 180 – 120 = 60 since consecutive angles are supplementary, so y = 12.
Therefore 3y + 28 = 36 + 28 = 64. But the angles marked 5y and 3y + 28 should be congruent, which is not the case.
Therefore this cannot be a parallelogram.
Triangles
The main results about triangles are these:
1. The angles of a triangle add to 180o.
2. An exterior angle of a triangle equals the sum of the two remote interior angles:
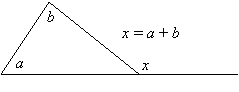 |
3. The base angles of an isosceles triangle are congruent, and conversely:

4. The side opposite the smallest angle in a triangle is the shortest side and the side opposite the largest angle is the longest side, and conversely.
EXAMPLE 5:
One angle of a triangle is twice as large as another angle, and the third angle is 20o less than the largest angle. What are the measures of the angles in this triangle?
SOLUTION: We can let x and 2x denote the measures of two angles.
Then 2x – 20 is the measure of the third angle.
Since the angles add to 180o, we can write the following equation:
(x) + (2x) + (2x – 20) = 180
Solving: 5x – 20 = 180, 5x = 200, x = 40
The angles are:
x = 40o
2x = 80o
2x – 20 = 60o
EXAMPLE 6: Find the measure of angle ABC:
 |
SOLUTION:
The external angle is the sum of its two remote interior angles, so we can write the following equation:
4x + 24 = 2x + 3x
Solving, we find that x= 24.
Therefore the exterior angle measures 4 . 24 + 24 = 120o.
Angle ABC is supplementary to this, so it measures 180 – 120 = 60o.
EXAMPLE 7: Which side is longest in the following triangle?
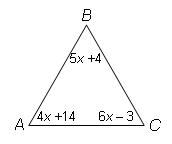
SOLUTION: First we solve for x:
4x + 14 + 5x + 4 + 6x – 3 = 180
15x + 15 = 180
15x = 165
x = 11
Now we find the angles:
angle A: 4x + 14 = 58o
angle B: 5x + 4 = 59o
angle C: 6x – 3 = 63o
Since angle C is the largest angle, side AB is the longest side.
Polygons
A polygon of n sides can be partitioned into n – 2 non-overlapping triangles with vertices in common with the polygon. For example, a quadrilateral has 4 sides and can be split into 2 triangles, and a triangle has 3 sides and consists of 1 triangle.
Since the angles of a triangle add to 180 degrees, the angles of an n-sided polygon must add to 180(n – 2) degrees.
EXAMPLE 8: Find the measure of angle A in the following pentagon:
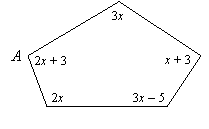 |
SOLUTION:
A pentagon has 5 sides, so can be partitioned into 3 triangles:
 |
Therefore its angles add to 3 times 180o, so
(2x + 3) + (3x) + (x + 3) + (3x – 5) + 2x = 3 . 180
11x + 1 = 540
11x = 539
x = 49
So angle A measures 2 . 49 + 3 = 101o
Return to Lesson 3