Dilations and Similarity

A dilation is a transformation that stretches or shrinks a figure to create a similar figure.  Dilations have a "center of dilation" and a "scale factor."  The scale factor can be positive or negative, and its absolute value is the ratio of the length of any segment between two points of the image to the length of the corresponding segment in the preimage.

In general, a dilation with center O and scale factor k maps a point P onto a point Q according to the following rules:

(1)  If k is positive, then Q is on the ray from O through P, and OQ = k∙OP

(2)  If k is negative, then Q is on the ray opposite ray OP, and OQ =  –k∙OP

(3)  The center O is mapped onto itself.

(4)  The dilation is called an expansion if the absolute value of k is greater than 1.

(5)  The dilation is called a contraction if the absolute value of k is less than 1.

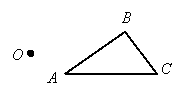
Example 1:  Find the image of triangle ABC under the dilation with center O and scale factor 3.

Solution:  From O we draw segments through each vertex and extend them by 3 times their original length.  Then we draw the image triangle (labeled with primes):

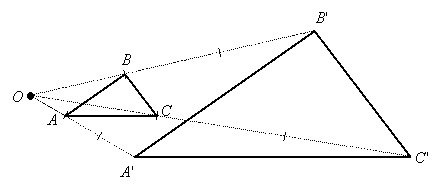Example 2:  Find the image of triangle PQR under the dilation with scale factor -½ and center O:

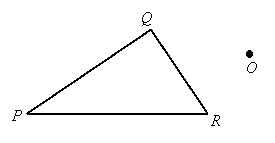Solution:  We draw segments from O to the vertices of the triangle and extend them in the opposite direction by half their lengths to determine the vertices of the image (labeled with primes):

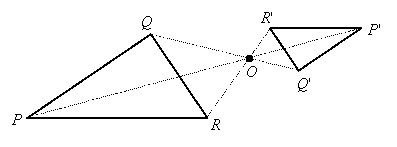If the scale factor in Example 2 were –1 instead of -⅛ then the image would be congruent to the preimage, so the dilation would be an isometry.  It would be equivalent to a rotation of 180^o about O.

Example 3:  The figure shows a segment and its image under a dilation.  What is the scale factor of that dilation?

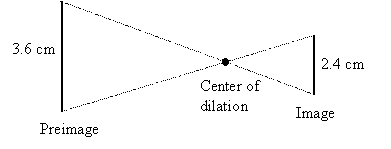Solution:  The image is in the opposite direction of the preimage, so the scale factor is negative.  If the scale factor is k, then 3.6k = –2.4, so

Return to Lesson 5