Classifications of 3-dimensional Objects

Basic Solids

In geometry the basic three dimensional objects can be classified according to whether they have flat surfaces or curved surfaces.

A three-dimensional shape whose faces are polygons is known as a polyhedron. This term comes from the Greek words poly, which means "many," and hedron, which means "face." So a polyhedron is a three-dimensional object with many faces.  The faces are polygons whose sides are edges and whose vertices are vertices of the polyhedron.  Cubes and pyramids are examples of polyhedra (plural of "polyhedron"):

The standard objects with curved surfaces are cylinders, cones and spheres:

Prisms

A prism is a polyhedron in which two faces are parallel and congruent polygons, called its bases and whose other faces are parallelograms, called its lateral faces.  The edges of the lateral faces are called lateral edges of the prism and are parallel and congruent.  A prism also has an altitude, which is the perpendicular distance between the planes of the bases:

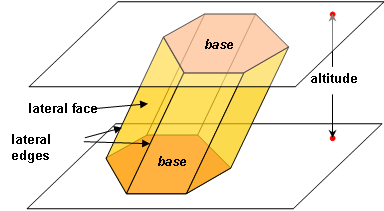
Prisms are often classified by the shape of their bases.  Thus a triangular prism is a prism whose bases are triangles, and a hexagonal prism is a prism whose bases are hexagons. A right prism is a prism in which its lateral edges are perpendicular to its bases.  In this case the lateral faces are rectangles:

Lateral Area

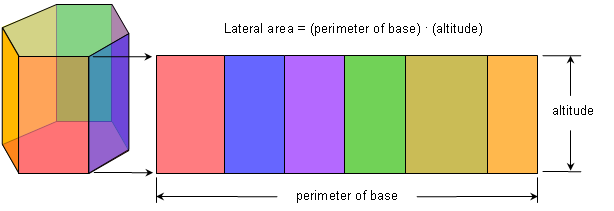
The lateral area of a prism is the total area of its lateral faces.  For a right prism, this area is equal to the perimeter of a base times its altitude, since the lateral faces can be "unwrapped" to form a rectangle:

Lateral area of a right prism:

Pyramids

A pyramid is a polyhedron for which one face, called the base, is a polygon and all other faces, called lateral faces, are triangles.  As with prisms, pyramids are often classified by the shapes of their bases.  Thus a triangular pyramid is one in which the base is a triangle and a square pyramid is one in which the base is a square.  If the base is the "bottom" of the pyramid, the "top point" is called its apex.  If the base is a regular polygon and all the faces are congruent isosceles triangles, then the pyramid is called a regular pyramid.

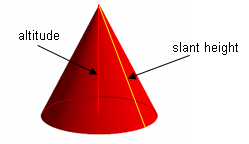
The segment from the apex perpendicular to the base of a pyramid is called its altitude.  Sometimes the length of this segment is also called the altitude.  In a regular pyramid, a segment from the apex perpendicular to a side of the base (or the length of that segment) is called the slant height.

The lateral surface area of a pyramid is the total area of its lateral faces.  For a regular pyramid, this area is equal to ½ of the slant height times the perimeter of the base.

Cylinders

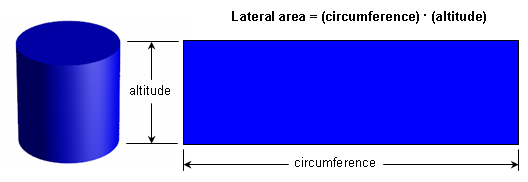
A cylinder is like a prism except that its bases are circles instead of polygons.  A right cylinder is a cylinder in which the segment joining the centers of the circular bases is perpendicular to the bases.  The lateral area of a right cylinder is equal to the circumference of a base times the altitude, since a cylinder can be "unwrapped" to give a rectangle:

Cones

A cone is like a pyramid except that its base is a circle instead of a polygon.  A right cone is a cone in which the line from the apex to the center of the base is perpendicular to the base.  As with pyramids, cones have an altitude (perpendicular from the apex to the base) and right cones have a slant height which is a segment from the apex to the circumference of the base.

Platonic Solids

A Platonic solid is a regular, convex polyhedron.  Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex. They have the unique property that the faces, edges and angles of each solid are all congruent.  There are only 5 regular Platonic solids, named according to the number of faces, the tetrahedron (4 faces), the hexahedron (common cube with 6 faces), the octahedron (8 faces), the dodecahedron (12 faces), and the icosahedron (20 faces):

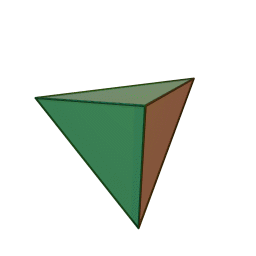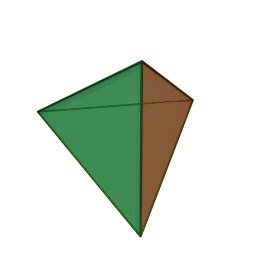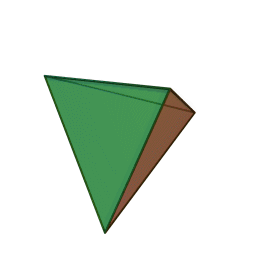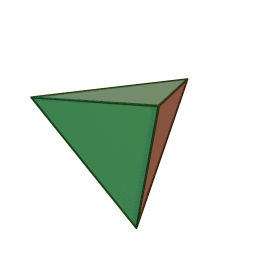
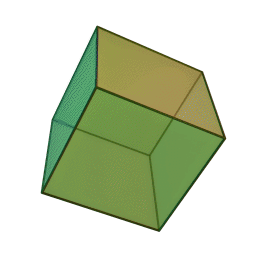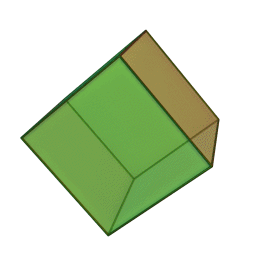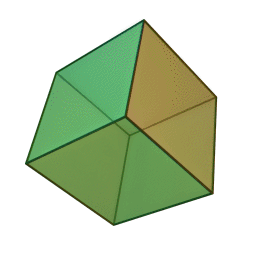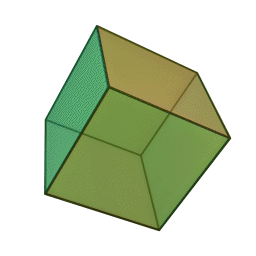
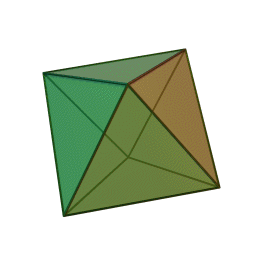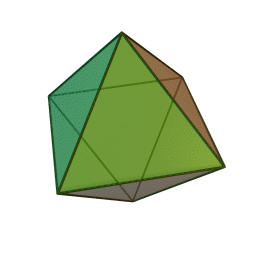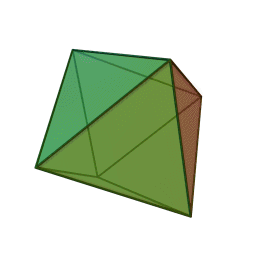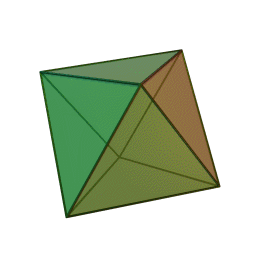
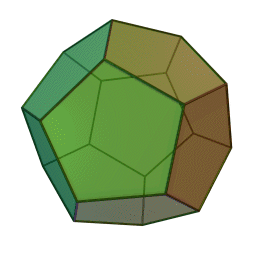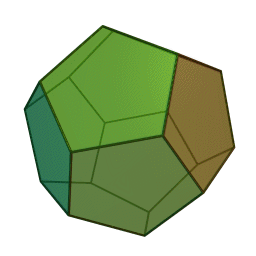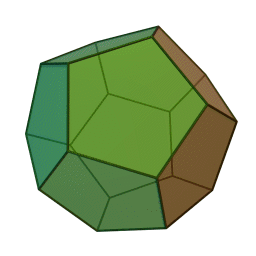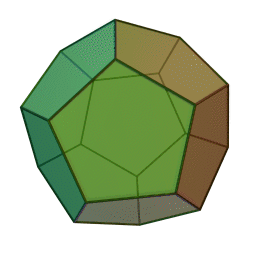
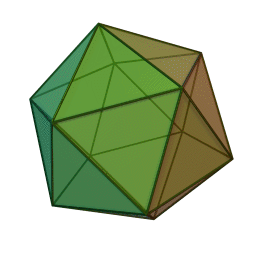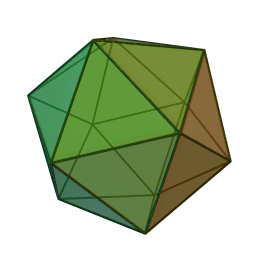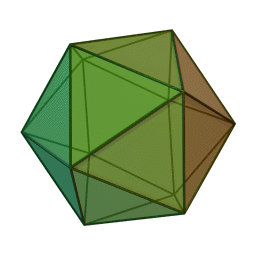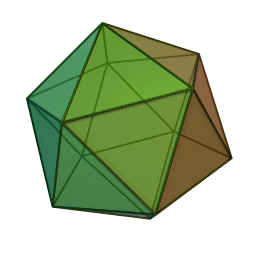
They are named for the ancient Greek philosopher Plato.  He wrote about them around 360 B.C. and associated each of the four classical elements (earth, air, water, and fire) with four of these.  Earth was associated with the cube, air with the octahedron, water with the icosahedron, and fire with the tetrahedron.

Detailed information about and animated pictures of the Platonic solids can be found at the Wikipedia website. http://en.wikipedia.org/wiki/Platonic_solid .