Basic Linear Equations

Simple Linear Equations

A linear equation in one unknown is an equation in which the unknown appears only to the first power.  If the unknown is x, then the only operations that involve x are multiplication or division by a number and addition or subtraction of numbers.  That is, a linear equation in x does not contain x in the denominator of a fraction, it does not contain a root of x or a power of x other than the first power.  For example,

2(x – 3) + 5x = 7 – x

is a linear equation in x, but

3x² + 5 = 2x

is not since it has an x² in it.

A linear equation in one unknown is like a scale.  It has two sides (a left side and a right side) with the equals-sign between them.  We could represent the unknown by a cylinder, and numbers by marbles:

An equation is solved when the unknown is by itself on one side of the equation and the other side has only a number.  In terms of the scale, the cylinder is on one side and the other side has only marbles.  The steps in solving an equation must correspond to keeping the scale balanced.

The following examples illustrate the scale idea in solving linear equations.

Example 1:  7 = x + 2

This equation can be represented by the following scale:

The unknown is on the right pan of the scale, and we need take away two marbles to get it by itself.  But if we take away 2 marbles from the right pan, then we must also take away two marbles from the left pan to keep the scale balanced:

This corresponds to subtracting 2 from both sides of the equation:

7 – 2 = x – 2

So we have:

5 = x

That is, the solution is x= 5.

Example 2:  2x + 5 = 3x

This time x is on both sides of the equations, and the scale looks like this:

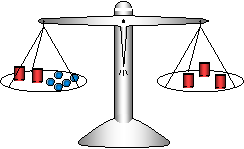
We must take away two x's from both sides:

As for the equation, we subtract 2x from both sides:

2x + 5 – 2x = 3x – 2x

Again we get 5 = x, so x = 5 is the solution of the equation.

Example 3:  3x + 2 = 2x + 6

Again x is on both sides, and the scale looks like this:

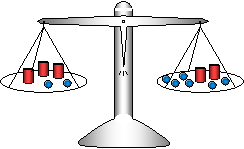
First we will remove two x's from both pans, and then remove two marbles from both pans:

In solving the equation we perform two steps:

(1)  Subtract 2x from both sides:  3x + 2 – 2x = 2x + 6 – 2x

This leaves x + 2 = 6

(2)  Subtract 2 from both sides:  x + 2 – 2 = 6 – 2

This leaves x = 4 as the solution.

Inverse Operations

The scale model illustrates the main principle involved in solving an equation:

Whatever you do to one side, you must do the same to the other side.

The strategy is always to isolate the unknown on one side of the equation.  If a number is added to the unknown, then you subtract that number.  If the unknown is on both sides, then you subtract the smaller term so it is only on one side.

In general, you "undo" what is done to the unknown so it becomes isolated.  This undoing requires you to apply what is called "inverse operations."  The idea is simple:  If something is added, you subtract.  If something is subtracted, you add.  If something is multiplied, you divide, and if something is divided, you multiply.

For example, the inverse of "add 3" is "subtract 3."  Likewise, the inverse of "divide by 3" is "multiply by 3."

The following examples illustrate the use of inverse operations in solving equations:

Example 4: Solve 13x = 182

Solution:  "13x" means "13 times x."  The inverse of "multiply by 13" is "divide by 13," so we divide both sides of the equation by 13:

So x = 14.

Example 5:  Solve the following equation:

Solution:  x is divided by 4.  The inverse of "divide by 4" is "multiply by 4," so we multiply both sides of this equation by 4:

This gives us x = 48

To see that this makes sense, we "check" the solution by replacing x with its value, 48:

This says 48 divided by 4 equals 12, and that is correct.

Example 6: Solve  x – 7  =  19

Solution:  The inverse of "subtract 7" is "add 7," so we add 7 to both sides of this equation:

x – 7 + 7 = 19 + 7

So x = 26

Again we can "check" the solution:  26 – 7 = 19

Example 7:   Solve  7 – x = 19

Solution:  In this problem, x is subtracted.  The inverse of "subtract x" is "add x," so we will start by adding x to both sides:

7 – x + x = 19 + x

This gives 7 = 19 + x, which is the same as 7 = x + 19.

Now we see that 19 is added to x, so we subtract 19 from both sides:

7 – 19 = x + 19 – 19

–12 = x

That is, x = –12

Another method is to rewrite the equation by representing subtraction as "addition of the opposite":

7 – x = 19 is equivalent to 7 + (–x) = 19 or (–x) + 7 = 19.

Then subtract 7:  (–x) + 7 – 7 = 19 – 7

This gives (–x) = 12, or –x = 12.

–x is equal to –1x, so we can divide by –1:

So x = –12 as before.

Let's check this:  7 – (–12) = 7 + 12 = 19

Equations with x on both sides

When the variable is on both sides of the equation, it is usually best to begin by eliminating the variable from one side.

Example 8: Solve 3x – 20 = 5x

Solution:  We can think of this as 3x + (–20) = 5x, or –20 + 3x = 5x

We subtract 3x from both sides:  –20 + 3x – 3x = 5x – 3x

This leaves –20 = 2x, and then we divide by 2 to get –10 = x.

So x = –10

Check:  3(–10) – 20 = 5(–10)?  Yes, because –30 – 20 = –50.

Example 9:  Solve 6x – 17 = 15 – 2x

Solution:  First add 2x to both sides:  6x – 17 + 2x = 15 – 2x + 2x

This leaves 8x – 17 = 15

Then add 17:  8x – 17 + 17 = 15 + 17

So 8x = 32

Finally divide by 4 to get x = 4

Check:  6(4) – 17 = 15 – 2(4)?   Yes, because 24 – 17 = 15 – 8 and both differences are 7.

Return to Lesson 1