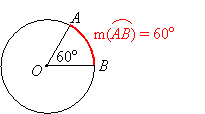
Arc Measure
Meaning of Arc Measure
Arcs are measured in degrees. This is not the same as the length of an arc, which depends on the size of the circle.
The measure of a minor arc is defined as the measure of its central angle:
|
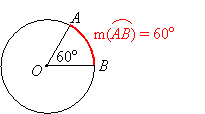The measure of a major arc is 360o minus the measure of the corresponding minor arc:
 |
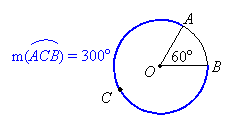Lengths of Arcs
The measure of an arc is given in degrees. The length of an arc depends on the size of the circle and is measured in standard units, such as inches, centimeters, etc. The circumference of a circle is an arc measuring 360o. The length of the circumference is given by the formula: C = πd, where d is the diameter of the circle. This formula can also be given as: C = 2πr, where r is the radius. An arc measuring θ degrees is θ /360 of the circumference, so its length can be found by either of these formulas:
or
Example 1: Find the length of a 72o arc in a circle of radius 10 cm.
Solution:
length = 72/360 Χ 20π = 4π cm or about 12.57 cm
Area of a Sector
A sector of a circle is the region enclosed by an arc and two radii to its endpoints:
 |
Since the area of a circle is given by A = π r2, the area of a sector whose arc measures θ degrees is given by the formula:
A "Slice"
Example 2: Find the area of the shaded slice:
 |
Solution: The area of the shaded region can be found by subtracting the area of the triangle from the area of the sector:
 |
The triangle consists of two 30-60-90 triangles, so its sides and altitude can be determined:
 |
The area of the sector is 120/360 times 36π cm2, or about 37.7 cm2. The area of the triangle is:
So the area of the desired slice is about 37.7 – 15.6 = 22.1 cm2.
Inscribed Angles
An inscribed angle is an angle with its vertex on the circle and whose sides are chords of the circle:
 |
When a side of an inscribed angle contains a diameter of the circle, it is easy to see that the measure of the inscribed angle is half the measure of its intercepted arc:
 |
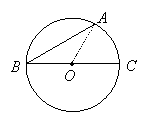because triangle AOB is isosceles (BO and AO are radii). But
because an external angle of a triangle is the sum to the two remote interior angles. Therefore 
. But the measure of arc AC is the same as the measure of the central angle, AOC.
The Measure of an Inscribed Angle
In general, the measure of the inscribed angle is half the measure of its intercepted arc:
 |
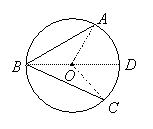Angle ABD measures half of arc AD and angle DBC measures half of arc DC. Therefore angle ABC measures half of arc ADC.
We state this as a theorem:
Theorem 3: The measure of an inscribed angle is half the measure of its intercepted arc:
 |
Two Inscribed Angles with the Same Arc
An important consequence of this is:
Theorem 4: If two inscribed angles incept the same arc, then they are congruent.
 |
Since angles ABD and ACD both intercept arc AD each measures half that arc, so they have the same measure and are therefore congruent.
Example 3: What is the measure of arc ABC?
 |
Solution: Since angle ADC is an inscribed angle, it is half its intercepted arc. Therefore the measure of that arc is twice this angle, or 160o.
Arcs of Intersecting Chords
If two chords intersect, their vertical angles are congruent, and each vertical angle is the average of the two intercepted arcs:
 |
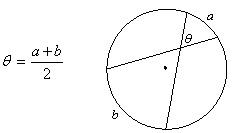We can prove this result by joining endpoints of the chords to form a triangle with q as an exterior angle:
 |
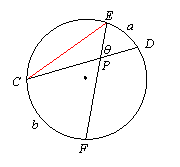θ is an exterior angle of triangle CEP, so it is the sum of the two remote interior angles, angles ECD and CEF. But these are inscribed angles with intercepted arcs whose measures are a and b, so each measures half its arc:
Arcs Intercepted by Secants
In the following figure, PT and QT are secants to circle O. The measure of angle T is related to the measures of arcs PQ and RS by the given formula:
 |
The proof of this is similar to the proof that the measure of the angle formed by two intersecting chords is the average of intercepted arcs.
In triangle QRT, angle PRQ is an exterior angle, so it is equal to the sum of its remote interior angles:
But angle PRQ is an inscribed angle, so its measure is half of its intercepted arc, of half of a. Likewise, angle RQT is also an inscribed angle, so it measures half of b. Substituting these in the above equation gives us:
Therefore,
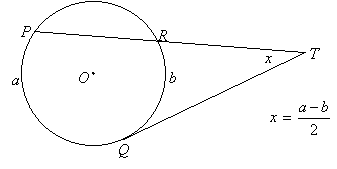
Arcs Intercepted by Tangents and Secants
If one of the secant lines is moved away from the center of the circle until it becomes a tangent line, the same result holds:
 |
The same is true about two tangents with a common external point:
 |
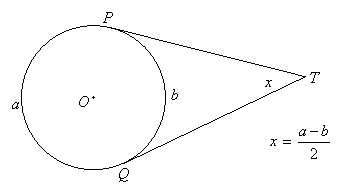In fact, since a + b = 360o, this last result can also be written as:
or as
Return to Lesson 5