Triangle Angle-Bisector Theorem

An Angle Bisector in a Triangle

Suppose we have an isosceles triangle and bisect the vertex angle.  This bisector cuts the base at its midpoint.

However, if the triangle is not isosceles, then it is not obvious how an angle bisector cuts the opposite side.

Proportional Segements

The Triangle Angle-Bisector Theorem gives a simple result about how an angle bisector cuts the opposite side in a triangle, and follows from the Proportional Segments Theorem (a result about parallel lines cut by a transversal).  Recall that if lines L1, L2 and L3 are parallel and cut by transversals L4 and L5, then the segments on these transversals are proportional:

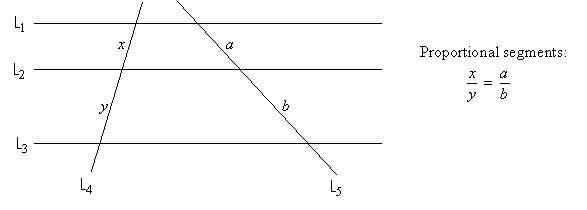
To see how this result relates to the bisector of an angle in a triangle, extend parallels at the other vertices (at A and C, where  bisects ):

Then extend one of the sides adjacent the bisected angle until it meets both parallels.

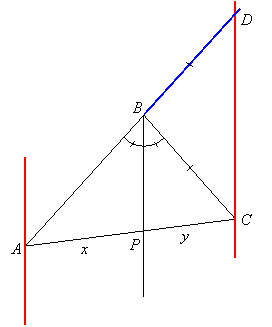
By properties of parallel lines (alternate interior angles and corresponding angles) it is easy to show that , so BC = BD (by the Isosceles Triangle Theorem).

 In the diagram,  and  are transversals cut by the 3  parallel lines, and

so . Since BD = BC, this gives:  .  That is, the bisector of an angle of a triangle splits the opposite side into segments with the same proportion as the adjacent sides.

The Triangle Angle-Bisector Theorem

If  bisects  in ,then .  That is,  in the figure on the right.

EXAMPLE:

Find the length value of x in the figure on the right:

 SOLUTION:     By the Triangle Angle-Bisector Theorem, .  Solving gives x = 6.