The Transitive Property of Congruence

The Transitive Property

If you take a train from Belen to Albuquerque, and then continue on that train to Santa Fe, you have actually gone from Belen to Santa Fe.  The transitive property is like this in the following sense:  If you know one angle is congruent to another, say , and that other angle is congruent to a third angle, say, then you know the first angle is congruent to the third:  .  Basically, the transitive property tells us we can substitute a congruent angle with another congruent angle.  This is really a property of congruence, and not just angles.  If two segments are each congruent to a third segment, then they are congruent to each other, and if two triangles are congruent to a third triangle, then they are congruent to each other.  So we can state the transitive property this way:

Transitive Property:    If two geometric objects are congruent to a third geometric object, then they are congruent to each other.

 

Applications

Problem 1:

Given:

paste_image98.gif

 

Prove:   is the midpoint of

Proof:  By the transitive property, it follows that  since both are congruent to .  Therefore  is the midpoint of  since the midpoint of a segment splits it into two congruent pieces.

Problem 2:

Given:

 

Prove:       bisects

Proof:     "Bisects" means "cuts in half," so we must show  cuts  into two equal angles. From the transitive property it follows that since they are both congruent to .  Therefore  bisects .

 

 

Problem 3:

Given:

 

 ,

lines L1 and L2 are parallel,

lines L3 and L4 are parallel

 

Prove: 

Proof:     Since L3 and L4 are parallel, , since they are alternate interior angles for the transversal L2.  Therefore  by the transitive property.  Since L1 and L2 are parallel,  since they are corresponding angles for transversal L4.  Applying the transitive property again, we have .

Complements and Supplements

Two rather obvious results similar to the transitive property are these: 

Theorem:  Complements of congruent angles are congruent.

Proof:     If two angles are congruent, then their measures are equal.  Let us call the common measure a.  Then a is a number between 0o and 180o.  Their complements are (90 – a)o, and so they are equal to.  Therefore their complements are congruent. 

 

Theorem:  Supplements of supplementary angles are congruent. 

The proof is essentially the same as for the previous theorem.

 

In addition, we can also state this rather obvious result:

 

The Reflexive Property of Congruence:

Any geometric object is congruent to itself.

 

Here are a couple of problems involving these concepts:

 

Problem 1: 

Given:

 and  are complements,  and  are complements

paste_image123.gif

Prove:

Proof:  Since  is congruent to itself (reflexive property),  and  are complements of congruent angles, so they are congruent.

Problem 2:

Given:  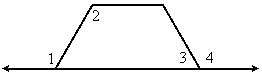,    and  are supplements

Prove: 

Proof:      and  are supplements because they form a linear pair.  Therefore (since  and  are supplements) .  Since , it follows that  by the transitive property.

Click here to return to the main Lesson 6 page.