Sum of Angles in a Triangle

Do the Angles Add Up to 180 Degrees?

You probably learned that the angles of any triangle add to 180^o.  But how do you know this is true?

First you need to understand exactly what a triangle is.  Of course you know one when you see one:  It has three sides and the sides are straight.

The meaning of "straight" is the first step to understanding the angles of a triangle.  Technically and angle is a ray, whereas the sides of a triangle are segments.  But when we talk about an angle of a triangle, we are referring to the rays that contain the angle.

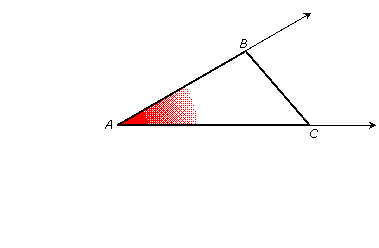
For example, angle A in the following triangle has rays  and  as its sides:

Making a Triangle with Straight Edges

The following movie clip shows how to be sure the edges of a triangle are straight.

It may take a few minutes to download, so be patient! When the movie finishes, hit the back-arrow on your browser.

Making a Triangle

Flatness

From the video clip, we see that a straight segment can be constructed by stretching a string between two points, as it is the path of shortest distance between those points.  When a triangle is constructed this way on a flat surface, the angles do seem to add to 180^o within a margin of measuring error.

But this is no proof that the angles will always add to 180^o, and it apparently has something to do with "flatness" as well as "straightness."  What if a triangle is constructed on a surface that is curved?

Triangle on a Sphere

The following movie shows how to make a triangle on a sphere. What do its angles add to?

It may take a few minutes to download, so be patient! When the movie finishes, hit the back-arrow on your browser.

Triangles on a Sphere

Triangle on a Cylinder

It seems that the angles of triangles constructed on curved surfaces will not add to 180^o.  But this is not necessarily true.

The following movie shows that triangles on some curved surfaces do have angles that add to 180^o.

It may take a few minutes to download, so be patient! When the movie finishes, hit the back-arrow on your browser.

Triangles on a Cylinder

Proving the Angles Add Up to 180 Degrees

The Parallel Postulate is the key to understanding why (and when) the angles of a triangle add to 180^o:

Parallel Postulate:

Given a line and a point not on that line, there is one and only one line through the given point that is parallel to the given line.

The proof that the angles of a triangle add to 180^o on any surface for which the parallel postulate holds is actually rather easy.  The idea is to draw a parallel line at one of the vertices and consider alternate interior angles:

Given:   and the parallel postulate

Prove:   

Proof:

By the parallel postulate, there is a line  containing point B that is parallel to side :

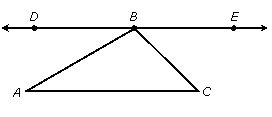
Now side  is a transversal for the parallel lines  and , so its alternate interior angles are equal:

Likewise, side  is a transversal for the parallel lines  and , so its alternate interior angles are also equal:

Looking at the top of this figure, we see that  because these angles form a line.  But  and , so the angles of the triangle add to 180^o.

Click here to return to the main Lesson 6 page.