Slope
The Coordinate System and Slope
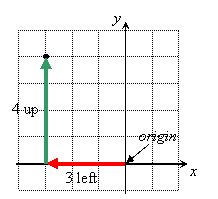
A point on a graph has an x-coordinate and a y-coordinate. x is always first and y is second. To plot a point, start at the origin (place where the x-axis and y-axis cross each other), move right or left, depending on whether the x-coordinate is positive or negative, and then move up or down, depending on whether the y-coordinate is positive or negative.
Example: The point (–3, 4) is plotted like this:
The slope of a line is the rate of change in y per change in x. This is expressed as a fraction of the form
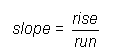
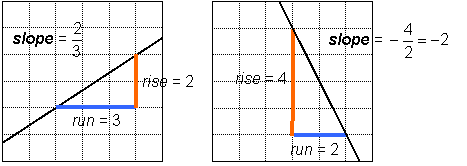
and is positive if the line goes uphill from left to right (y in increases when x increases) or negative if the line goes downhill from left to right (y decreases when x increases).
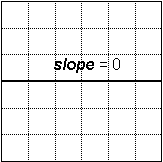
The slope is 0 if the line is horizontal (like a road). A vertical line (like a pole) has no slope.
A Road Analogy for Slope
To keep from getting confused about positive, negative, 0, and undefined slopes, think of a road with traffic going left to right. When the road is horizontal, the slope is 0. When the road goes uphill, the slope is positive and when it goes downhill the slope is negative. A vertical telephone pole isn't part of the road, so it has no slope.
Examples
|
1. |
This line has positive slope because it goes uphill.
|
|
|
2. |
This line has negative slope because it goes downhill.
|
|
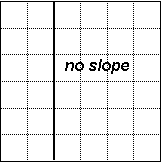
| 3. | This line has no slope because it is vertical. The fact that the x-intercept is 5 is irrelevant.
|
|
|
4. |
The slope of this line is 0 because it is horizontal. The fact that the y-intercept is 3 is irrelevant.
|
|
Click here to return to the main Lesson 7 page
