Scaling and Similarity

Similarity

Two figures are "similar" if one is a scaled-up or scaled-down version of the other.  It is also allowed that one is a scaled mirror image of the other.  For example, the two "houses" are similar.  The second is a scaled, mirror image of the first:

The "scaling factor" is the fraction you multiply linear measurements in the first by to obtain corresponding measurements in the second.  In the above pictures the scaling factor is 5/4 or 125%.  This means that any linear measurement in the second picture is 1.25 times as big as the corresponding measurement in the first.  (For example, if you measure the height of the door in the first picture, then the height of the door in the second picture is 1.25  times this measurement.)

You can find the scaling factor by measuring corresponding lengths in the two pictures and taking their ratio.  For example, if you measure the heights of the doors you may get: 

       First picture:   height of door =   0.4 in                   Second picture:  height of door = 0.5 in

Then the scaling factor is:

If the figures are similar, the same scaling factor (after the fraction is reduced) will result no matter which pair of corresponding measurements are made.  Thus if you measure the width of each house and recompute the scaling factor, you get:

        First picture:  width of house =  16 in            Second picture:  width of house =  20 in

Thus we can define similarity as:

            Two figures are similar if they have uniform scaling factors.

Areas

In lesson 1, we learned from Plato's Meno that when you double the length and width of a square the area is quadrupled. Scaling factors refer to linear measures and not areas. In general, when a figure is scaled by a factor of x, then the area is scaled by a factor of x².

For example, suppose a rectangle measures 4 inches by 6 inches, and we scale it by a factor of 3/2. Then the scaled rectangle measures 6 inches by 9 inches. The area of the first rectangle was 4 x 6 = 24 in², while the area of the second is 6 x 9 = 54 in². 

The ratio of these areas is

Thus the ratio of areas is the square of the scaling factor.

Ratios of Measurements

Another observation about similarity is that ratios of measurements are preserved.  For example, the height of the door to the width of the house in the first picture and form the ratio of these two measurements, then do the same in the second picture, the resulting ratios will be the same:

     First picture:  

     Second picture: 

 In addition, corresponding angles will be the same.  These observations give another characterization of similarity:

Two figures are similar if corresponding angles and ratios are the same.

When the two figures are triangles it is enough to know that corresponding angles are the same.  Furthermore, since the sum of the angles in a triangle is always 180^o, it is enough to know that two pairs of corresponding angles are the same.  This is known as the "AA-Theorem" in geometry.  For example, the following two triangles are similar by AA:

In this case we write:     The symbol means "is similar to."

Overlapping Figures

Some figures can be viewed as two overlapping similar figures.  For example, if lines BC and DE are parallel, the following can be viewed as two similar triangles,  and  since corresponding angles  and  are congruent, and the triangles have  in common:

As a consequence, suppose AB = 10, BD = 5 and AC = 14.  To find x = CE you need to consider whole measurements:  AB = 10, AD = 15, AC = 14, AE = 14 + x:

You can reduce the fraction on the left, then cross-multiply to find x:

,      ,    ,    ,   

Simplifying Ratios

Now a little algebra makes it possible to do this kind of problem more directly.  In the general case, let the segment-lengths be labeled as a, b, c, d:

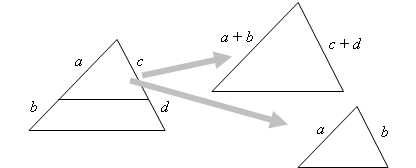
Then, equating the scaling ratios from larger to smaller triangle: 

Doing some algebra changes this equation to a simpler one: 

,     ,    so  .

We can turn these fractions upside down and also write: 

This gives us a theorem:

When a segment that joins two sides of a triangle is parallel to the third side it cuts the joined sides into proportional parts:

This argument can be extended to several parallel lines, and we can "chop off the top of the triangle" to get another theorem:

When three or more parallel lines intersect two transversals they cut off proportional segments: