The Pythagorean Theorem

Opening Question

If each grid-line in the graph is 1 cm long, then how long is the yellowish line?

13slant.png

Contrary to what you might think, it isn't 12 cm long. The next page shows one method to find the length of this slanting line.

Using a Compass to Find the Length of a Slanting Line

The lengths of horizontal and vertical lines on a graph are easy to determine, so we will draw two such lines to make a right triangle with the yellowish line:

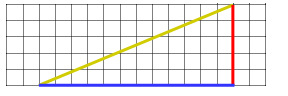
5_12.png

The blue line is 12 cm long and the red line is 5 cm long. To find the length of the yellowish line you could use a compass to swing it to the top like this:

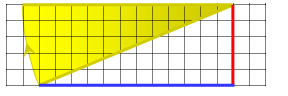
5_12_13.png

Now it is apparent that it is 13 cm long.

But how does the length of the yellowish line relate to the lengths of the blue and red lines?

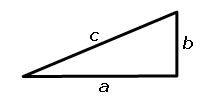general.png We formed a right triangle with the blue and red lines as its legs and the yellowish line as its hypotenuse. When using letters to name the sides of a right triangle, we usually label the legs as a and b, and the hypotenuse as c.

The Pythagorean Theorem

 

A secret to understanding the relation among the side-lengths (a, b and c) of a right triangle is to use areas.

 

PythA.gif

If we construct squares on the three sides of the triangle as in the picture, then the area of the yellow square is exactly equal to the combined areas of the blue and red squares. This is because the yellow square can be covered with 4 copies of the triangle and a little square, and the blue and red squares combined can be covered with the same 4 copies of the triangle and little square. To see why this is so, click on the picture.

 

In other words, c2 = a2 + b2

 

 

PythB.gif

Sample Problems

Problem 1

If each grid-line in the graph is 1 cm long, then how long is the slanting line?

 

prob1a.png

 

Solution

 

 

We draw the legs of the right triangle containing this line as its hypotenuse and then invoke the Pythagorean Theorem.

Both legs are 8 cm long, so c2  = 82 + 82 = 64 + 64 = 128.

Now the 128 is the square of the hypotenuse, so we use a calculator and take the square root to find c:

(This is an approximate value rounded off the the nearest hundredth.)

prob1b.png

Problem 2

The bottom of a 12-foot long ladder is 3 feet from the base of a wall against which it leans. How high up the wall does the ladder reach?

 

 

Solution

We draw a picture and then use the Pythagorean Theorem.

The height (h) of the ladder is a leg of the right triangle and the hypotenuse is 12. So our setup is:

122 = h2  + 32

That is, 144 =  h2  + 9, so h2  =  135. Using the square root key on a calculator, we fine that h  =  11.62. So the ladder will reach a height of about 11.6 feet.

prob2.png

Problem 3

Marshall is building a shed with a slanting roof. It is to be 6 feet wide, 5 feet in the back and 6 feet in the front when viewed from a side. How long should the slanting roof beams be?

 

prob3a.png

 

Solution

 

 

We move the base up to make a triangle at the top. This leaves 1 foot for the height of the triangle, and the roof beam is the hypotenuse. So the Pythagorean Theorem gives us:

x2 = 62 + 12 = 36 + 1 = 37.

Using the square root key on a calculator, we find that x = 6.0828 feet.

Since carpenters measure in feet and inches, it is best we convert this appropriately:

x = 6 ft + 0.0828 x 12 in = 6 ft + 0.993 in, or approximately 6 ft 1 in.

prob3b.png

 When you're done click here to return to the main Lesson 2 page.