Points, Lines, Planes and Sapce
Basic Building Blocks of Geometry
Geometry is based on a set of givens and uses deductive logic, called "proof," to establish conclusions. The "givens" are definitions and/or postulates, and the "conclusions" are called theorems or corollaries. (A "corollary" is a result that follows directly from a "theorem" and is easy to prove. It is like a "mini-theorem.")
Some terms in geometry are classified as "undefined" or "primitive." Euclid tried to define all terms he used, but not everything can be defined without going around in circles. Today we accept certain concepts as "primitive" and do not attempt to define them. The most basic are the terms point, line, plane, and space. We use postulates to give them meaning. Some of these postulates are:
- For any two points, there is exactly one line containing them.
- Every line contains at least two points.
- Every plane contains at least three points not all on the same line.
- Space contains at least four points not all in the same plane.
- If a plane contains two points of a line, then that plane contains the whole line.
- If a line intersects a plane that does not contain it, then it intersects the plane in exactly one point.
- Any three points lie in at least one plane, and any three points not on the same line lie in exactly one plane.
- If two planes intersect, their intersection is a line.
Now these postulates are necessary to give the proper meaning to the undefined terms. In particular, they captivate the notions of "straightness" and "flatness." Thus, lines are "straight" and planes are "flat." Intuitively we think of a point as a location. It has no width or thickness. A line separates a plane into two halves and has no width, and a plane separates space into two halves and has no thickness.
Since the concepts of "being on the same line" and "being in the same plane" are important in geometry, we use definitions to simplify them:
1. Definition: Two or more points are collinear if they all lie on the same line.
2. Definition: Two or more points are coplanar if they all lie in the same plane.
These definitions can be used to shorten postulates 3, 4 and 7:
3. Every plane contains at least three noncollinear points.
4. Space contains at least four noncoplanar points.
7. Any three points lie in at least one plane, and any three noncollinear points lie in exactly one plane.
Euclid tried to keep his list of postulates shorter than what you saw on the previous page, but it was later discovered that he made some additional assumptions, so more postulates were added to clarify the proofs. However, not everything that seems basic or "obvious" need be classified as a postulate, and mathematicians since Euclid try to keep the list as short as possible. For example, the following fact seems about as obvious and simple as any of the above postulates:
If two lines intersect, then they intersect in exactly one point.
But this in fact is a Theorem since it follows logically from postulate 1, and we can prove it using the contrapositive of that postulate provided we first translate the postulate to if-then form:
Postulate 1: If A and B are two different points, then there is exactly one line containing them.
Contrapositive: If there are no lines or more than one line containing points A and B, then A and B are the same point.
Thus, if points A and B are contained in both lines l and m, then they must be the same point.
Here is another theorem that seems as simple and obvious as a postulate:
There is exactly one plane containing a given line and point not on the line.
It can be proved directly using postulates 2 and 7:
Proof: By postulate 2, there are 2 points on the given line. Since the given point is not on that line, the given point is a 3rd point, and these three points are noncollinear. By postulate 7, these three points lie in exactly one plane.
These are not all the postulates of Euclidean geometry. Another postulate that Euclid gave (though in a slightly different form) is the so-called Parallel Postulate:
9. Given a line and a point not on that line, there is exactly one line containing the given point and parallel to the given line.
Euclid did not like this postulate because it seemed more complicated than the others, and for more than 1000 years people tried to prove it on the basis of the other postulates. Eventually it was understood that this postulate cannot be proved from the others, and it is possible to assume it false and derive a different kind of geometry (called "non-Euclidean"). In fact, the geometry Einstein used to describe gravitational forces in the universe is a form of non-Euclidean geometry. According to Einstein's Theory of Relativity, all lines in space eventually intersect, so there is no such thing as true parallel lines. But for all practical purposes, Euclidean geometry does work for most of the things we do (as in making buildings) and it is far simpler to use than Einstein's geometry. It is also more intuitive and easier to understand.
Postulates and Theorems Related to Planes
A plane goes on forever, so we can't really draw one. But we can draw a square piece of a plane to illustrate some of the postulates and theorems about planes. Here are the main facts:
|
(1)
|
The intersection of two planes is a line:
|

|
|
(2)
|
Three noncollinear points determine a plane:
|

|
|
(3)
|
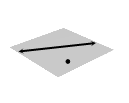
A line and a point not on that line determine a plane:
|
|
|
(4)
|
Two intersecting lines determine a plane:
|

|
|
(5)
|
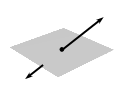
The intersection of a line and a plane not containing that line is a point:
|
|
|
(6)
|
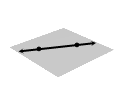
If a plane contains two points, then it contains the line through those two points.
|
|
|
(7)
|
It is possible for three or more planes to intersect in a line:
|
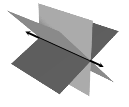
|
|
(8)
|
It is possible for three planes to intersect in a point:
|

|
|
(9)
|
It is possible for three noncoplanar lines to intersect in a point:
|
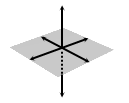
|
The Shed Problems
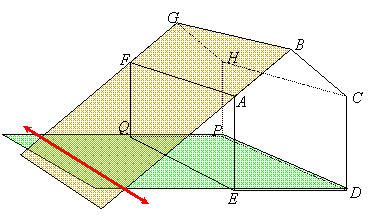
 The figure on the right is a 3-dimensional drawing of a shed with no doors or windows. Its roof, sides and floor are parts of seven different planes, which are referred to in the questions below. Planes ABC and FGH (containing the front and back walls) are parallel, as are planes FAE and HCD (containing the left and right walls). No other planes determined by the roof, walls or floor of this shed are parallel.
The figure on the right is a 3-dimensional drawing of a shed with no doors or windows. Its roof, sides and floor are parts of seven different planes, which are referred to in the questions below. Planes ABC and FGH (containing the front and back walls) are parallel, as are planes FAE and HCD (containing the left and right walls). No other planes determined by the roof, walls or floor of this shed are parallel.
1. Consider the front wall. It contains the 5 points A, B, C, D, E, and any three of these can be used to name the plane of this wall. For example, this plane can be named "plane ABC," it can be named "plane ACE," and so on. Give 4 other names of this plane.
2. Now consider the left part of the roof. This contains the points A, B, G, F. Its plane can be named by any three of these points. For example, it can be named as "plane ABC," "plane AFG," and so on. Give 2 other names of this plane.
3. The plane determined by the roof (plane AFG) and the plane determined by the floor (plane QED) eventually intersect, as the following picture shows:
What geometric object is the intersection of these two planes?
4. In general, if two different planes intersect, what geometric object is their intersection? (This is stated in one of the postulates.)
5. Consider the right wall which contains the points C, D, P, H. Its plane, plane DPH, intersects the line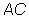 as shown:
as shown:
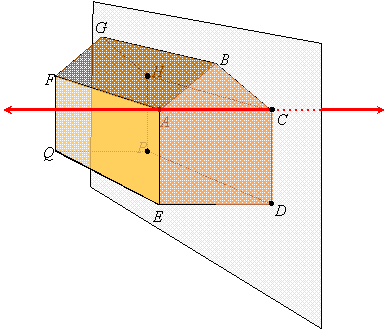
Name the intersection of plane DCH and line AC.
6. In general, what geometric object is the intersection of a plane and a line not entirely contained in the plane?
7. Now consider the plane determined by points E, C and H. Points E and C are on a diagonal across the front wall, so this plane slants and does not contain any of the walls, roof or floor of the shed. Name a fourth point that is coplanar with points E, C and H.

Answers
(1) plane ACD, plane ADE, plane BCE, plane CDE (more answers possible)
(2) plane ABG, plane BGF (more answers possible)
(3) a line (drawn in red)
(4) a line
(5) point C
(6) a point
(7) point Q
When you're done with this activity, click here to return to the main Lesson 4 page.









 The figure on the right is a 3-dimensional drawing of a shed with no doors or windows. Its roof, sides and floor are parts of seven different planes, which are referred to in the questions below. Planes ABC and FGH (containing the front and back walls) are parallel, as are planes FAE and HCD (containing the left and right walls). No other planes determined by the roof, walls or floor of this shed are parallel.
The figure on the right is a 3-dimensional drawing of a shed with no doors or windows. Its roof, sides and floor are parts of seven different planes, which are referred to in the questions below. Planes ABC and FGH (containing the front and back walls) are parallel, as are planes FAE and HCD (containing the left and right walls). No other planes determined by the roof, walls or floor of this shed are parallel.