Protractors and Angles
Protractors
You probably know that there are 360 degrees in a circle. But do you know why? It goes back about 4000 years ago. We inherited this number from the ancient Babylonians. They viewed the seasons as “circular,” and represented changes in a year around a circle. Though there are 365 days in a year, they wanted a number that is easier to work with. They also had a fancy for the number 60, and that is where we get 60 minutes in an hour. We also get 24 hours in a day from the ancient Babylonians.
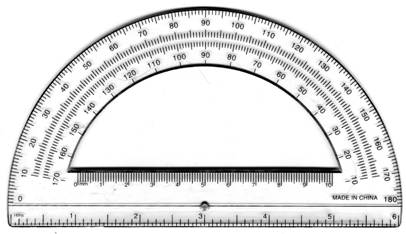
A protractor is a device for measuring angles. Most protractors are semicircles so they contain 180 degrees, like this:

But What Is an Angle?
You probably know an angle when you see one. In fact, the word “angle” derives from a Greek word for “elbow.” So an angle usually has a “bend” to it. In geometry we need to be a little more precise than that. An angle actually consists of two rays with a common vertex. There are no restrictions other than that. A ray is like a “half line” that it goes on forever, but in only one direction, and the point where it starts is called its “vertex.”
The rays that make up an angle are called its “sides” and it is important to realize that they have infinite length. Since we can’t draw things of infinite length, we are forced to draw the sides as segments. But the length of those segments is not an indication of how “large” an angle is. For example, both of these angles are the same size even though the angle on the left looks smaller because its sides are drawn smaller:

The “size” of an angle can be measured in degrees using a protractor. This is equivalent to drawing a circle centered at its vertex, dividing the circle into 360 equally-spaced marks and then counting the number of marks between the sides of the angle. If the sides are drawn too short to fit a protractor, you have to extend them. For example to measure the angle above (both drawings represent the same angle) you would place its vertex at the origin of the protractor and one side along the horizontal, like this:
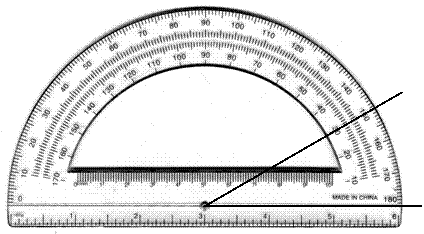
This angle measures 30 degrees.
Angles have an “interior” which is the region between the sides. More precisely, the interior of an angle is the region containing all segments that can be drawn connecting the two sides:

Classifications of Angles
When the rays of an angle are perpendicular, the angle measures 90 degrees.
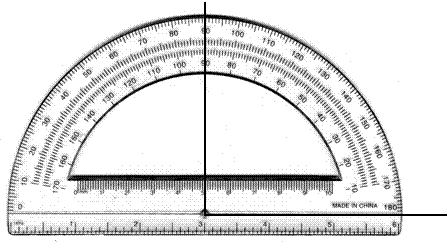
90 degree angles are called right angles.
One angle is smaller than another angle if it "fits inside" with both vertices at the same point. For example, the red angle is smaller than the blue angle:
Of course, the degree measure of the smaller angle will be less than the degree measure of the larger angle.
An angle that is less than 90o is called an acute angle, and an angle greater than 90o is called an obtuse angle.

Since any two rays with a common vertex form an angle, we could have an angle that measures as much as 180o when the rays point in opposite directions:

Such an angle is called a straight angle, and it is nothing more than a line.
Naming Angles
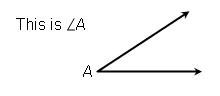
Angles can be named in several ways. The simplest is to label the vertex with a single letter preceded by a slanting L:
When angles share sides we can place numbers inside (close to the vertex). For example, angles 1 and 2 share the common vertex A:
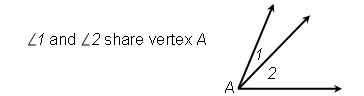
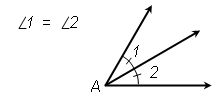
We also use little arcs centered at the vertex with tick-marks to indicate angles that have the same measure. Here angles 1 and 2 are equal (in measure):
You can also name an angle using three letters, where the middle letter is the vertex and the other two are points on the sides:
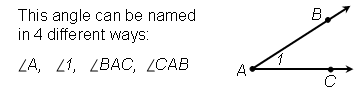
Click here to return to the main Lesson 3 page.