Parallel Lines and Transversal Angles

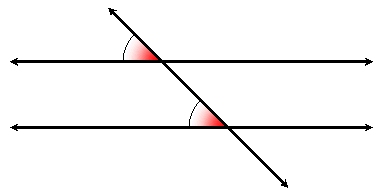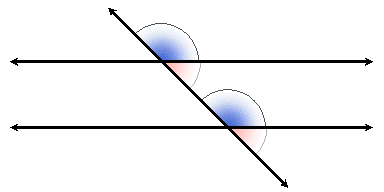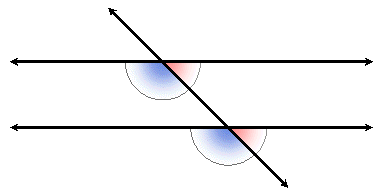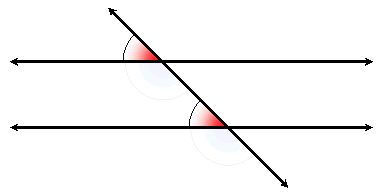
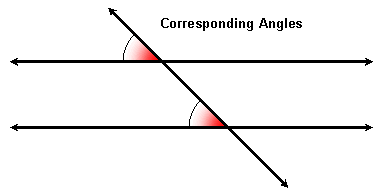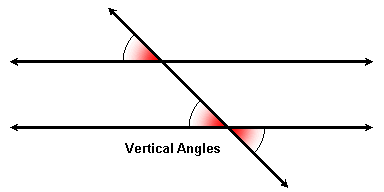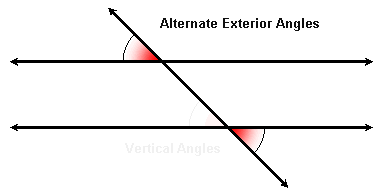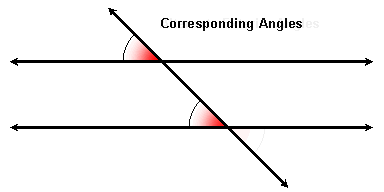
Corresponding Angles

Remember that 4 pairs of corresponding angles are formed when two parallel lines are cut by a transversal.  To find such a pair, think of taking a picture at one of the intersections and moving it to the other:

If the lines are parallel, then corresponding angles are congruent. Conversely, if the corresponding angles are congruent then the lines are parallel.

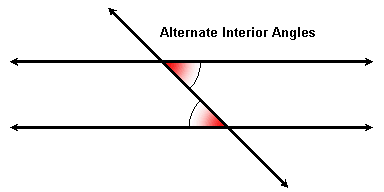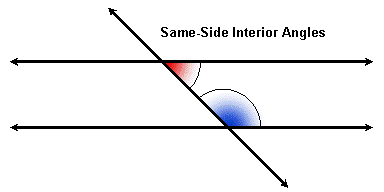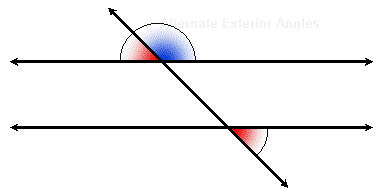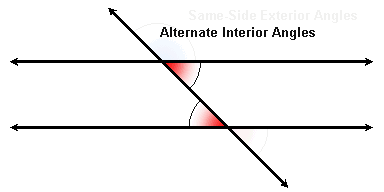
Alternate Interior Angles

Since vertical angles are congruent, we can use the transitive property to replace one of two corresponding angles with its vertical angle.  This gives us a pair of alternate interior angles:

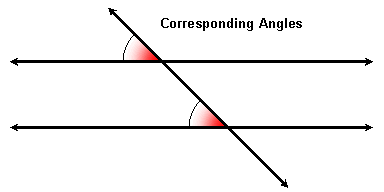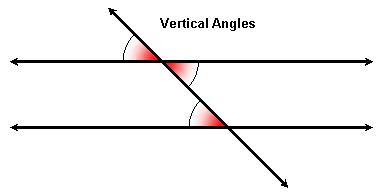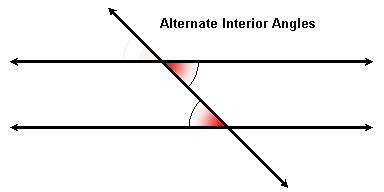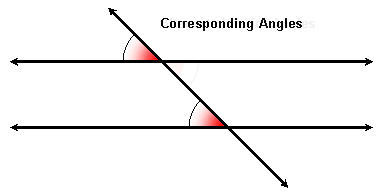
The "alternate" refers to the fact that they are on alternate sides of the transversal, and the "interior" refers to the fact that they are between the two parallel lines.

As with corresponding angles, alternate interior angles are congruent if and only if the two lines are parallel.

Alternate Exterior Angles

As with alternate interior angles, we can replace one of two corresponding angles with its vertical angle.  This gives us a pair of alternate exterior angles.

Again the word "alternate" means they are on opposite sides of the transversal, and "exterior" means the are not between the parallel lines (they are "outside").

Two lines are parallel if and only if alternate exterior angles are congruent.

Same-Side Angles

If two angles form a line, they are called a "linear pair," and their measures add to 180^o.  In other words, they are supplementary.

If we replace one of a pair of alternate interior angles with its linear supplement, we get a pair of same-side interior angles, and if we replace one pair of alternate exterior angles with its linear supplement, we get a pair of same-side exterior angles.

Same-side interior angles and same-side exterior angles are supplementary if and only if the two lines are parallel.

Proofs

These results can be used to prove two lines are parallel or to prove results about angles formed by a transversal cutting parallel lines.

Example 1:

Given:	,
Prove:

Proof:

 and  are alternate interior angles for lines AC and DE with transversal CE, so sides AC and DE are parallel.  Likewise,  and  are alternate interior angles for lines AE and CD with transversal AD, so sides AE and CD are parallel.  Therefore ABCD is a parallelogram because its opposite sides are parallel.

Example 2:

Given:	Angles P and Q are supplementary.
Prove:	Side PS is parallel to side QR.

Proof: 

Angles P and Q are same-side interior angles for lines PS and QR with transversal PQ.  Since these angles are supplementary, sides PS and QR must be parallel.

Example 3:

Given:	is supplementary to , line is parallel to line
Prove:

Proof:

 and  are same-side interior angles for lines  and .  Since these lines are parallel,  and  are supplementary.  Since  is also supplementary to  and  is congruent to itself (reflexive property),  (supplements of congruent angles are congruent).

Click here to return to the main Lesson 6 page.