The Hinge Theorem
What is the Hinge Theorem?
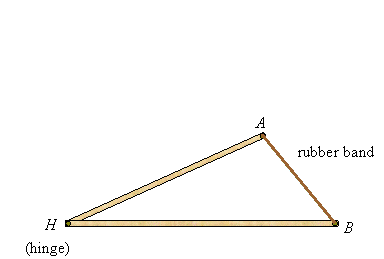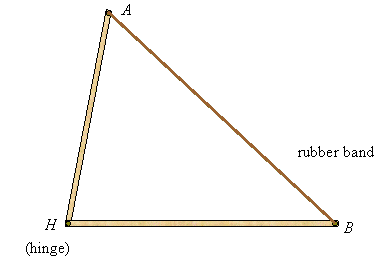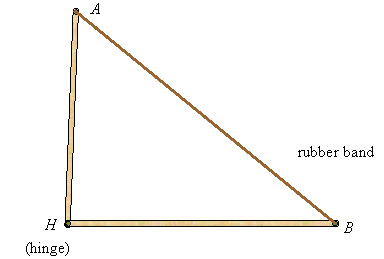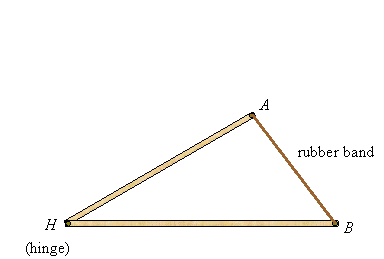
Suppose you take two sticks (not necessarily of the same lengths), hinge them at a common end, and attach a rubber band at the other ends. Then you can open and close them to form triangles as the following illustrates:
When comparing two triangles with two pairs of congruent sides, you see that the triangle with the larger angle between those sides has the larger third side, and conversely:
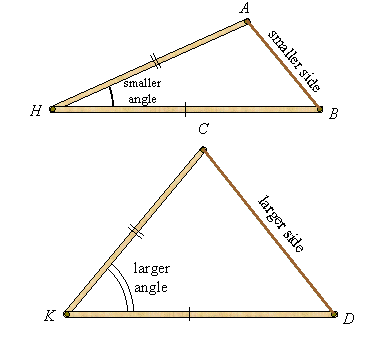
This result is known as:
The Hinge Theorem
If in 
and 
, 
and 
then 
if and only if 
.
The result is rather obvious if you think of the rubber band idea, and we will not prove it here. Instead we will consider some examples.
Examples
Example 1:
If  is the median of  and  , then it follows from the Hinge Theorem that  , and therefore  : |
 |
Example 2:
If  is equilateral,  , and  , it follows from the Hinge Theorem that sides  and  are shorter than the equal sides  ,  and  . This is because  and  so each measures less than 60o. Therefore  is the largest angle in  , which makes side  the largest side in that triangle. |
 |
Example 3:
Jan and Jon are hikers. They start at the visitor center and walk in opposite directions for 2 miles. Then Jan turns to her right at an angle of 20o, and Jon turns to his right at an angle of 30o. They each continue hiking for another mile and a half when both stop to rest. Who is farther (as the crow flies) from the visitor center?
Solution:
Draw the segments from each person's final position to the visitor center, and find the supplementary angles formed by their turning angles. Then you have two triangles, 
and 
, with 
and 
:
Since 
, it follows from the Hinge Theorem that 
, so Jan is farther from the visitor center.