Coordinate Proofs

Introduction to Coordinate Proofs

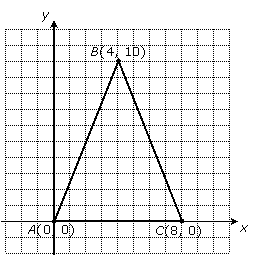
An isosceles triangle is a triangle with two congruent sides.  For example, the triangle with vertices A(0, 0), B(4, 10), and C(8, 0) is isosceles:

If we want to be absolutely sure, we could prove it is isosceles by using the distance formula to show the lengths of sides AB and BC are equal:

This might seem like killing a fly with a sledge-hammer.  After all, B's x-coordinate is halfway between A's and C's, and the picture makes it clear.

Suppose we draw segments from vertices A and B to the midpoints of their opposite sides:

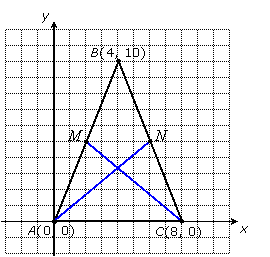
These segments are called medians of the triangle, and also happen to be congruent.

The coordinates of the midpoints are:

The lengths of the segments are:

So these two medians are congruent.

This suggests that the two medians connecting the congruent sides of any isosceles triangle might be congruent.  To prove that assertion, we need to consider a more general isosceles triangle.  No matter what triangle we consider, we can call the base-length 4b, (we can choose 4 times a number so midpoints will come out easier) and we can place the base along the x-axis with one vertex at the origin and the other at (4b, 0).  In our above triangle, the base-length was 8, so b = 2.  The third vertex will have coordinates (2b, something), and we can make the "something" equal to 2c, where c is some number:

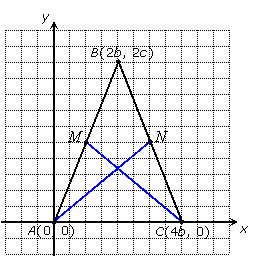
Then the midpoints (by the midpoint formula) have coordinates:  M = (b, c) and N = (3b, c).  Now we can use the distance formula to prove that AN = CM:

The idea behind a coordinate proof is to place the figure in question on the xy-plane at a convenient location, and assign general coordinates (with variables) to its important points.

Specific Polygons

A "specific polygon" is already placed on the xy-coordinate plane and the coordinates of its vertices are known.

Example:

The vertices of a quadrilateral are A(0, 0), B(2, 6), C(10, 12), D(8, 0):

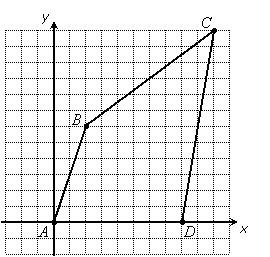
Prove that the quadrilateral formed by joining the midpoints of its sides is a parallelogram.

Solution:

We use the midpoint formula to find the coordinates of the midpoints and draw the quadrilateral that joins the midpoints.  Call this quadrilateral MNPQ:

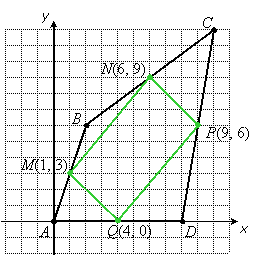
To prove this quadrilateral is a parallelogram, we show pairs of opposite sides are parallel.  All we have to do is show their slopes are equal:

Since these are the same, we know side MN is parallel to side PQ.  We must also show side MQ is parallel to side NP:

Again the slopes are equal, so side MQ is parallel to side NP, and therefore quadrilateral MNPQ is a parallelogram.

Proofs about General Polygons

The last problem was interesting.  We started with a lopsided quadrilateral and joined the midpoints of its sides to form another quadrilateral which turned out to be a parallelogram.  This suggests a Theorem, which we can prove using coordinates:

Theorem: 

If the midpoints of the sides of a quadrilateral are joined to form an inscribed quadrilateral, then that inscribed quadrilateral is a parallelogram.

Proof:

We can place one of the sides along the positive x-axis with its vertex, A, at the origin and label the coordinates of the other vertex, B, as (2b, 0), where b is some number (it is half the length of that side).  We can label the other vertices as C(2c, 2e) and D(2d, 2f) where c, e, d, and f are numbers, not necessarily all positive:
Now we use the midpoint formula to find the midpoints of the sides: Finally we use slope to prove sides MN and PQ are parallel: and we can use slopes to prove sides NP and QM are also parallel: So quadrilateral MNPQ is a parallelogram since its opposite sides are parallel.

An Angle Inscribed in a Semicircle

A semicircle is half a circle.  If you choose a point P on the semicircle and draw segments to the endpoints of the diameter, you end up with an angle inscribed in a semicircle:

Now it looks like a right angle.  Let's prove it is a right angle in a special case.  To prove it in general requires a strong foundation in algebra, so we won't attempt that here.

Let's suppose the circle has radius 10.  We place the semicircle at the origin, and suppose the x-coordinate of P is 6.  We will call the y-coordinate b for the time being.

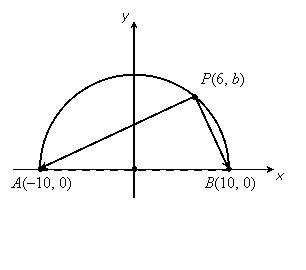We need to know the y-coordinate of P.  The equation of a circle of radius r centered at the origin is x² + y² = r², and since P is on the circle, the coordinates 6 and b are related by this equation, 6² + b² = 10².  Solving for b we get b = 8.  So P has coordinates (6, 8).

Now to prove the angle at P is a right angle, we can show the slopes of lines AP and BP are opposite reciprocals:

So the slopes are opposite reciprocals, and therefore the angle at P is a right angle

Click here to return to the main Lesson 8 page.