Proofs involving CPCTC

CPCTC

The main reason for proving two triangles congruent is to prove parts of those triangles are congruent.  Recall that a triangle congruence such as  means six things.  Three pairs of sides are congruent and three pairs of angles are congruent:

,

Study the following problems carefully so you understand the details.  Proofs are given in statement-reason format and in paragraph format.

Problem 1

Given:    and  is the midpoint of

Prove:   is the midpoint of

Note:  The symbol  means "is parallel to."

Proof:

In paragraph form, we could write the proof like this:

It is given that .  Therefore  since these are alternate interior angles for transversal .  Since  is the midpoint of , .  We also know  since these are vertical angles.  Therefore  by ASA, and so  since these are corresponding parts of the congruent triangles.  Thus  is the midpoint of .

Problem 2

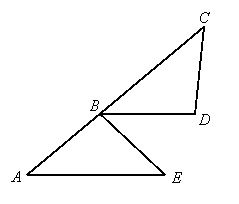
Given:   ,  , and

Prove: 

 Proof:

In paragraph form we can write:

Since , , and , it follows that  by SAS.  Therefore  since these are corresponding parts of the congruent triangles.  These are corresponding angles for  and  with transversal , so .

Problem 3

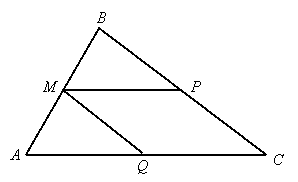
Given:   is the midpoint of ,  , and

Prove: 

Proof:

This proof is tricky.  Paragraph form might make it clearer:

Since  is the midpoint of ,  .  Since ,  since these are corresponding angles for the parallel lines with transversal .  We also know , so  by SAS.  Therefore  since these are corresponding parts of the congruent triangles.  Now if we consider transversal  for parallel lines  and ,  since these are corresponding angles.  Now since  and , it follows that  by the transitive property.  But these are corresponding angles for lines  and  with transversal , so .

Click here to returnt to the main Lesson 10 page.